Number Sets

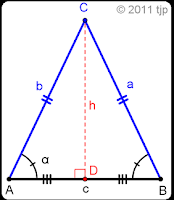
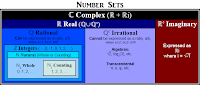
Couldn't find a complete and accurate Venn diagram of the sets of numbers, so here you go.

A couple of things to note:

• Natural numbers may be Whole numbers or Counting numbers. It depends on the application. The only difference is that Whole numbers includes zero while Counting numbers do not. It is not that either is a subset of Natural numbers — it's just either one or the other.

• There is no uniformly recognized symbol for Irrational numbers. Suffice it to say that Irrational numbers are all of the Real numbers that are not rational. In the universe of Real numbers, Irrational numbers are the complement of Rational numbers.

• Likewise, there is no uniformly recognized symbol for Imaginary numbers. In the universe of Complex numbers, Imaginary numbers are the complement of Real numbers.

• So all numbers are Complex? It turns out to be arguably so.
Given the form a + bi, where a and b are elements of the Real number set,
then
 for a pure Imaginary number, a = 0;
and
 for a pure Real number, b = 0.

Finding quadratic equation

1. Given three points, solve system of three equations using general form:
(1)   y₁ = ax₁² + bx₁ + c
(2)   y₂ = ax₂² + bx₂ + c
(3)   y₃ = ax₃² + bx₃ + c
to find (a, b, c)

2. Given two x-intercepts, p and q, and a point, solve for "a" using intercept form:
y = a(x - p)(x - q)

3. Given vertex, (h, k), and a point, solve for "a" using vertex form:
y = a(x - h)² + k

Distance between point and line

A foundational exercise in algebra is finding the distance between a given point and a given line.
SOP for doing this involves about three simple, intuitive steps. For some situations, however, a single-step solution is desirable.
I've generally left out intermediate steps just to keep the page from being filled with a lot of calculations. If you want to skip even the small bit posted here, you can go right to the bottom line. It won't hurt my feelings.

Given:
Line y = mx + b
and
Point (p, q)

1.
Perpendicular slope = -1/m

1a.
Use point-slope form to find perpendicular line:
y - q = -1/m(x - p)
y = (p + qm - x)/m

2.
Find abscissa of the intersection of given and perpendicular lines:
mx + b = (p + qm - x)/m
x = (p + qm - bm)/(m² + 1)

2a.
Find ordinate of that intersection:
y = m(p + qm - bm)/(m² + 1) + b
y = (b + m(p + qm))/(m² + 1)

2b.
Intersection Point:
(x, y) = ((p + qm - bm)/(m² + 1), (b + m(p + qm))/(m² + 1))

3.
Use distance formula to find distance, h, between (p, q) and intersection point:
h² = (p - (p + qm - bm)/(m² + 1))² + (q - (b + m(p + qm))/(m² + 1))²
h = √((b + mp - q)² / (m² + 1))

Isosceles Triangle (ASA)

Since h is the perpendicular bisector of the base line,
it is the side opposite the given angle, and
the length of adjacent side AD is known.
So
h = c tan(α) / 2

Three Known Sides (SSS)

Cosine Rule
a² = b² + c² - 2bc cos(α)
α = acos((c² + b² - a²) / (2bc))

Sine Rule
h/sin(α) = b/sin(90°)
h = b sin(α)

Executive Summary
h = b sin(acos((c² + b² - a²) / (2bc)))

Basic rules of exponents

There's only a handful of rules to remember about exponents.
I've never seen them named anywhere, so names shown are not "official."
•  b⁰ = 1 ← zero power rule
    note: invalid for b = 0
•  b¹ = b ← identity rule
•  a^m = b^m ⇔ a = b ← equal exponents
•  b^m = bⁿ ⇔ m = n ← equal bases
•  a^m × b^m = (ab)^m ← distributive rule
•  b^m × bⁿ = b^{(m + n)} ← product rule
•  b^m / bⁿ = b^{(m - n)} ← quotient rule
    note: b^-1 = 1/b
•  (b^m)ⁿ = b^(mn) ← power rule
    note: does not apply to b^(mn) which is b^mn
•  ⁿ√(b^m) = b^(m/n) ← root rule
    e.g. √ b = sqrt(b) = b^(1/2)

Practical Trig

Most all of the trig I have used in real life has been in connection with machine shop production: CNC mill and lathe programming and CAD design.
Nearly all trig problems can be solved with just four formulas:

with hypotenuse known:
OPP = HYP·sin(θ)
ADJ = HYP·cos(θ)

with either leg known
OPP = ADJ·tan(θ)
ADJ = OPP / tan(θ)

CNC mill problems are usually hypotenuse/angle problems (converting bolt patterns to x-y coordinates)
CNC lathe problems are usually leg problems (converting chamfers and tapers to x-z coordinates)