Crossing the river

A common problem for calculus students is what might be called the "crossing the river" problem. It involves crossing a river (or some other obstacle) with unequal cost (time, effort, etc.) to negotiate (travel, build, etc.) the river vs. negotiating the land. So the goal is to optimize the path.

Example:
Suppose the path to construct a refinery pipeline comes to a
perfectly straight and uniform river at some point, with the refinery
across the river, some distance upstream.
Suppose the river is 1 unit wide, and the refinery is 8 units
upstream. Also suppose the relative cost (per unit distance) for
constructing the pipeline in/over/under water is 1.6 that of
constructing it over land.

First, define in terms of distance:
Let
P = point pipeline reaches river
Q = point on opposite bank directly across river from P
R = location of refinery
S = some point on the opposite bank between Q and R
x = distance from S to R

see
crossing the river (path)

Given
PQ is 1 unit
QR is 8 unit
then
QS = 8 - x
and
Using pythagorean distance formula:
PS = √(1² + (8 - x)²)
PS = √(x² - 16x + 65)
domain 0 ≤ x ≤ 8

Second, define in terms of cost:

Given

relative cost on land = 1

relative cost in water = 1.6

Let

C(x) = total relative cost of pipe

C(x) = x + 1.6√(x² - 16x + 65)

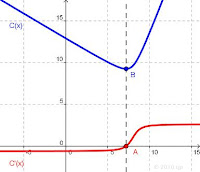
Third, solve:

C(x) is minimized when C'(x) = 0, so

C'(x) = 0.8(2x - 16) / √(x² - 16x + 65) + 1
0 = 0.8(2x - 16) / √(x² - 16x + 65) + 1
⋮
yadda yadda
⋮
1.56x² - 24.96x + 98.84 = 0
Apply quadratic formula to find:
x ≈ 7.1994 (discard spurious root out of domain)

So
The pipeline crosses river to a point ≈ 7.2 km from refinery.