How to define a circle with three points

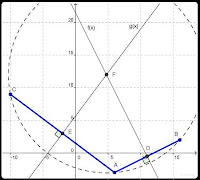
I was told this was a helpful way to understand how use three points to find a circle in a cartesian matrix. This method is based on the principle that the perpendicular bisectors of any two chords intersect at the center of the circle, so if you know this method you can stop reading or skip to the bottom line. I know there are more elegant ways to solve this problem, but this seems intuitive to me.

Let the points be:
A = (6, -3)
B = (16, 2)
C = (-10, 9)

Consider AB, AC and BC. By definition, each would be a chord of the circle to be found. I'll use AB and AC, but the final result would be the same for any two of them.

Let
D = Midpoint of AB:
D = (11, -1/2) *
Slope of AB = 1/2 †
Let
f(x) = line ⊥ to AB, through D:
• (y + 1/2) = -2 (x - 11) ‡
• y = -2x + 43/2
f(x) = -2x + 43/2

Let
E = Midpoint of AC:
E = (-2, 3) *
Slope of AC = -3/4 †
Let
g(x) = line ⊥ to AC, through E:
• (y - 3) = 4/3(x + 2) ‡
• y = 4x/3 + 17/3
g(x) = 4x/3 + 17/3

Let
F = center of circle to be found
F = f(x)∩g(x)
• -2x + 43/2 = 4x/3 + 17/3
• x = 19/4
• y = 4(19/4)/3 + 17/3 = 12
F = (19/4, 12)

Let
r² = square of distance from F to any of A, B or C. I'll use A:
r² = (6 - 19/4)² + (-3 - 12)² **
r² = 25/16 + 225
r² = 3625/16

SO
using standard circle form:
(x - h)² + (y - k)² = r²
where (h, k) = F,
resultant circle is:
(x - 19/4)² + (y - 12)² = 3625/16
or
(x - 4.75)² + (y - 12)² = 226.5625


The bottom line:

Let the three points be:
A = (h, k)
B = (p, q)
C = (v, w)
(k≠q and k≠w)

Then the perpendicular bisectors of AB and AC are:
ƒ(x) = (h² - 2 h x + k² - p² - q² + 2 p x) / (2k - 2q)
and
g(x) = (h² - 2 h x + k² - v² - w² + 2 v x) / (2k - 2w)

Use ƒ(x)∩g(x) to find center of circle @ ((α, β):
α = (h² (q-w) + k² (q - w) + p²w + q²w - q v² - q w² + k (v²+w²-p²-q²)) / (2(p w - q v + h (q - w) + k (v - p)))
and
β = ƒ(α) = (h² - 2 h α + k² - p² - q² + 2 p α) / (2k - 2q)
(it doesn't matter if you use ƒ(α) or g(α))

The radius of the circle (if you're interested) is:
√((h - α)² + (k - β)²)

And the circle is:
(x - α)² + (y - β)² = (h - α)² + (k - β)²
_______________
* midpoint formula: ((x₁ + x₂)/2, (y₁ + y₂)/2)
† slope formula: m = (y₁ - y₂) / (x₁ - x₂)
‡ point-slope formula: (y - y_n) = m(x - x_n)
** distance formula: c² = (x₁ - x₂)² + (y₁ - y₂)²