Parabolas: converting general ↔ vertex form

When working with quadratics, it is commonly desirable to convert general form (x²) quadratic functions such as:
• y = ax² + bx + c
into vertex form functions:
• y = a(x - h)² + k
and vise versa.

(Note that some sources refer to one or the other of the above forms as "standard" form. Hopefully that doesn't cause confusion here. It's the concepts that count, not the names.)

SOP for conversion from general to vertex form is "completing the square." This is the same technique used to derive the quadratic formula, a common exercise for first-year algebra students.

y = ax² + bx + c ← in this case, y ≠ 0
y - c = ax² + bx
(y - c) / a = x² + b/a x ← get x² "naked"
(y - c) / a + b²/(4a²) = x² + b/a x + (b/(2a))²
(y - c) / a + b²/(4a²) = (x + b/(2a))²

(y - c) / a = (x + b/(2a))² - b²/(4a²)
y - c = a(x + b/(2a))² - b²/(4a)
y = a(x + b/(2a))² - b²/(4a) + c
y = a(x + b/(2a))² + (4ac - b²)/(4a)
so
• h = -b/(2a)
• k = (4ac - b²)/(4a)

The reverse process is equally straight forward.
Expand vertex form to find general form:
y = a(x - h)² + k
y = a(x² - 2hx + h²) + k
y = ax² - 2ahx + ah² + k
y = (a)x² + (-2ah)x + (ah² + k)

so
• a = a
• b = -2ah
• c = ah² + k


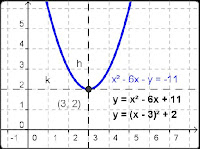
Example 1 (convert vertex to general form)

Given vertex form:
y = (x - 3)² + 2
convert to general form.
• a = 1
• h = 3
• k = 2
so
b = -2ah = -2(1)(3) = -6
c  = ah² + k = (1)(3)² + (2) = 11
so general form is:
y = x² - 6x + 11

Example 2 (convert general to vertex form)

Given general form:
y = x² - 6x + 11
convert to vertex form.
• a = 1
• b = -6
• c = 11
so
h = -b/(2a) = -(-6) / (2(1)) = 3
and
k = (4ac - b²)/(4a) = (4(1)(11) - (-6)²) / (4(1)) = 2
and so
vertex form is:
y = a(x - h)² + k
   = (1)(x - (3))² + (2)
y = (x - 3)² + 2