
Math uses many symbols that find their origins in disparate cultures throughout history. Often designed to provide visual clues about the relationships of terms and operations to be performed, they were not optimized for the limitations of plain computer text.*
A standard for representing such expressions as plain text is yet to be established, and the collection here is hardly complete. Be assured, however, it includes little that is new. These expressions have been seen frequently enough "in the wild," and so should be well-recognized by anyone familiar with the mathematical concept(s) involved.
Generally, take cues from the way expressions are entered into calculators, spreadsheets, BASIC, etc., and always pay strict attention to operation precedence (described by PEMDAS mnemonic). If you not sure you will be understood, provide a glossary of the notations you are using.
A standard for representing such expressions as plain text is yet to be established, and the collection here is hardly complete. Be assured, however, it includes little that is new. These expressions have been seen frequently enough "in the wild," and so should be well-recognized by anyone familiar with the mathematical concept(s) involved.
Generally, take cues from the way expressions are entered into calculators, spreadsheets, BASIC, etc., and always pay strict attention to operation precedence (described by PEMDAS mnemonic). If you not sure you will be understood, provide a glossary of the notations you are using.
Addition and subtraction
• m + n
• m - n
For subtraction, just use the symple hyphen (minus) character. Avoid en-dash, –, em-dash, —, horizontal bar, ―, or other alternative (about a half dozen altogether) even though they might look better.
• m + n
• m - n
For subtraction, just use the symple hyphen (minus) character. Avoid en-dash, –, em-dash, —, horizontal bar, ―, or other alternative (about a half dozen altogether) even though they might look better.
Multiplication
m × n or m · n is expressed as:
• m * n
or just
• m n
Avoid "x" or "×" for simple multiplication because it is easily confused with the common variable, x.
m × n or m · n is expressed as:
• m * n
or just
• m n
Avoid "x" or "×" for simple multiplication because it is easily confused with the common variable, x.
Division, proportions, ratios
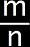 , m : n, or m ÷ n are all expressed by:
, m : n, or m ÷ n are all expressed by:
• m / n
Note: grouping can be significant:
m + n / p ≠ (m + n) / p
m / n·p ≠ m / (n·p)
• m / n
Note: grouping can be significant:
m + n / p ≠ (m + n) / p
m / n·p ≠ m / (n·p)
Relation Operators (comparison operators)
The easy ones are in the plain text character set:
• = equal
• < less than
• > greater than
≤ less than or equal
• <=
≥ greater than or equal
• >=
≠ not equal
Some common variations on this. These seem most widely used/recognized:
• <> (from BASIC, etc.)
• != (from C, etc.)
The easy ones are in the plain text character set:
• = equal
• < less than
• > greater than
≤ less than or equal
• <=
≥ greater than or equal
• >=
≠ not equal
Some common variations on this. These seem most widely used/recognized:
• <> (from BASIC, etc.)
• != (from C, etc.)
Exponents and Logarithms
mⁿ use the ^ (caret) for superscript:
• m^n
• m^(p/q)
Note that m^(p/q) ≠ m^p/q. Example:
4^(3/2) = 8
4^3/2 = 32
logbm = n use the _ (underscore) for subscript:
• log_b(m) = n
mⁿ use the ^ (caret) for superscript:
• m^n
• m^(p/q)
Note that m^(p/q) ≠ m^p/q. Example:
4^(3/2) = 8
4^3/2 = 32
logbm = n use the _ (underscore) for subscript:
• log_b(m) = n
Surds (irrationals, radicals, roots, etc.)
Plus or minus (±):
• +/-
Square root (√m):
• sqrt(m)
Cube root (∛m):
• cbrt(m)
Greater roots:
• express as rational exponents,
Example:
m^(1/4) (∜m)
• 4th-rt(m), 5th-rt(m), etc., should also be recognizable
π (ratio of circumference / diameter):
• pi (≈ 3.1415926)
Note: approximately 355/113 (≈ 3.1415929)
e (natural or exponential constant):
• e (≈ 2.7182818)
Note: always lower case
Φ (golden ratio):
• Phi { (1+√[5])/2 ≈ 1.6180340 }
Note: upper case P
φ (inverse of golden ratio):
• phi { 2/(1+√[5]) ≈ 0.6180340 }
Note: lower case p
Plus or minus (±):
• +/-
Square root (√m):
• sqrt(m)
Cube root (∛m):
• cbrt(m)
Greater roots:
• express as rational exponents,
Example:
m^(1/4) (∜m)
• 4th-rt(m), 5th-rt(m), etc., should also be recognizable
π (ratio of circumference / diameter):
• pi (≈ 3.1415926)
Note: approximately 355/113 (≈ 3.1415929)
e (natural or exponential constant):
• e (≈ 2.7182818)
Note: always lower case
Φ (golden ratio):
• Phi { (1+√[5])/2 ≈ 1.6180340 }
Note: upper case P
φ (inverse of golden ratio):
• phi { 2/(1+√[5]) ≈ 0.6180340 }
Note: lower case p
Grouping
For most interesting expressions, it's necessary to explicitly show grouping.
• ( and ) — round brackets or parentheses, are universally recognized, but it's easy to get lost when reading them.
Example:
y - ((x/tan(α-δ) – (h + r*cos(α–δ)) + (k – r*sin(α–δ))(tan(α–δ)))/tan(α–δ))
Sometimes it helps to use other grouping symbols:
• [ and ] — square or box brackets
• { and } — curly brackets or braces
Example:
y - {(x/tan[α-δ] – (h + r*cos[α–δ]) + (k – r*sin[α–δ])(tan[α–δ]))/tan[α–δ]}
Some care needs to be taken because box brackets and braces have specific meanings beyond simple grouping in certain mathematical expressions.
Note:
‹ and › — angle brackets are avoided as grouping symbols because they are commonly seen as inequality operators: < and >.
and
| and | — vertical lines (pipes) are not used as simple grouping operators because they are used to indicate absolute value, Euclidian distance, etc.
[ and ] — box brackets are sometimes used to indicate subscripts, the floor function, etc.
Polynomials
Factors with multiple terms must be grouped:
• (m + n) (p + q)
• (m + n) / (p + q)
Note:
(m + n)(x + y) / (p + q) = ((m + n)(x + y)) / (p + q)
but:
(m + n) / (x + y)(p + q) ≠ (m + n) / ((x + y)(p + q))
(m + n) / (p + q) / (x + y) / (w + z) ≠ ((m + n) / (p + q)) / ((x + y) / (w + z))
Factors with multiple terms must be grouped:
• (m + n) (p + q)
• (m + n) / (p + q)
Note:
(m + n)(x + y) / (p + q) = ((m + n)(x + y)) / (p + q)
but:
(m + n) / (x + y)(p + q) ≠ (m + n) / ((x + y)(p + q))
(m + n) / (p + q) / (x + y) / (w + z) ≠ ((m + n) / (p + q)) / ((x + y) / (w + z))
Scientific notation
Frequently, scientific notation is handwritten as: m × 10ⁿ which is convenient enough on a white board or paper. When superscipts and special characters aren't convenient, it becomes: m*10^n. This can get tedious and confusing when a number of terms get strung together, especially with negative exponents.
Examples:
6.626*10^(–34)
6.022*10^23
Better to use calculator / spreadsheet style notation:
• 6.626E–34 (5 fewer characters)
• 6.022E+23 (2 fewer characters)
Note: Use capital E to avoid confusion with exponential constant, e. Also, always express sign, + or -.
Frequently, scientific notation is handwritten as: m × 10ⁿ which is convenient enough on a white board or paper. When superscipts and special characters aren't convenient, it becomes: m*10^n. This can get tedious and confusing when a number of terms get strung together, especially with negative exponents.
Examples:
6.626*10^(–34)
6.022*10^23
Better to use calculator / spreadsheet style notation:
• 6.626E–34 (5 fewer characters)
• 6.022E+23 (2 fewer characters)
Note: Use capital E to avoid confusion with exponential constant, e. Also, always express sign, + or -.
Special Functions
• sqrt(x) — Square Root
• log_b(m) or log[b](m) — Log (base b) of m
• log(m) — Log (base 10) of m (common log)
• ln(m) — Log (base e) of m (natural log)
• abs(m) or |m| — Absolute Value
• sin(m) — Sine
• cos(m) — Cosine
• tan(m) — Tangent
• cot(m) — Cotangent
• sec(m) — Secant
• csc(m) — Cosecant
• sqrt(x) — Square Root
• log_b(m) or log[b](m) — Log (base b) of m
• log(m) — Log (base 10) of m (common log)
• ln(m) — Log (base e) of m (natural log)
• abs(m) or |m| — Absolute Value
• sin(m) — Sine
• cos(m) — Cosine
• tan(m) — Tangent
• cot(m) — Cotangent
• sec(m) — Secant
• csc(m) — Cosecant
Derivatives and integrals, summation, use braces because the contained function likely uses grouping:
• D{f(x)}or {f(x)}' — Derivative of the function ƒ(x): ƒ'(x)
• int{f(x)} — Indefinite integral of ƒ(x)dx: ∫{ƒ(x)}dx
• int{a, b, f(x)} — Definite integral of ƒ(x)dx over interval [a, b]
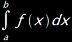
• sum{i=1, n, f(i)} — Summation, for i = 1 to n, of some ƒ(i)
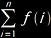
• D{f(x)}or {f(x)}' — Derivative of the function ƒ(x): ƒ'(x)
• int{f(x)} — Indefinite integral of ƒ(x)dx: ∫{ƒ(x)}dx
• int{a, b, f(x)} — Definite integral of ƒ(x)dx over interval [a, b]
• sum{i=1, n, f(i)} — Summation, for i = 1 to n, of some ƒ(i)
* Plain Text Characters:
10 numbers:
• 0 - 9
26 lower case letters:
• a-z
26 upper case letters:
• A-Z
27 symbols:
• ~ (tilde)
• ! (exclamation point, baseball bat)
• @ (at)
• # (pound, number, hash, octothorp)
• % (percent)
• ^ (caret)
• & (ampersand, and)
• * (asterisk, star)
• () (left and right parentheses, round brackets)
• - (hypen, dash, minus)
• _ (underscore, underline)
• + (plus)
• = (equal)
• [] (left and right box brackets, square brackets)
• {}(left and right braces, curly brackets)
• \ (slash)
• ; (semi-colon)
• : (colon)
• , (comma)
• < (less than)
• . (dot, period)
• > (greater than)
• / (forward slash)
• ? (question mark)
10 numbers:
• 0 - 9
26 lower case letters:
• a-z
26 upper case letters:
• A-Z
27 symbols:
• ~ (tilde)
• ! (exclamation point, baseball bat)
• @ (at)
• # (pound, number, hash, octothorp)
• % (percent)
• ^ (caret)
• & (ampersand, and)
• * (asterisk, star)
• () (left and right parentheses, round brackets)
• - (hypen, dash, minus)
• _ (underscore, underline)
• + (plus)
• = (equal)
• [] (left and right box brackets, square brackets)
• {}(left and right braces, curly brackets)
• \ (slash)
• ; (semi-colon)
• : (colon)
• , (comma)
• < (less than)
• . (dot, period)
• > (greater than)
• / (forward slash)
• ? (question mark)

No comments:
Post a Comment