Basic rules of logarithms

There is a lot of stuff on the web about logarithms. Here's a digest of the most essential facts. Seems no matter how much I use logs, my head still swims if I try to reason them out. Seems best to just memorize these few simple rules without thinking about them too much.

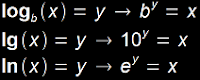
Nomenclature:
• log_b(x) → "log, base b, of x"
   log[b](x) is also recognizable when "b" is complicated
• ln(x) → natural log: "log, base e, of x"
• ld(x) or lb(x) → binary logarithm: "log, base 2, of x"
• Log(x) → "log, base 10, of x"
• log(x)  → common log: may be base e, base 10, or base 2
                   depending on location, application, context, etc.

Definitions:
• log_b(x) = y ⇔ x = b^y
• ƒ(x) = log_b(x)
   for {b∈ℝ | b > 0, b ≠ 1} and {x∈ℝ | x > 0}

Trivial identities:
• log_b(b) = 1
• log_b(1) = 0

Logarithm property of equality:
Ok, there really isn't such a property. Logs are exponents, so it's just the multiplication property of equality at work. None the less:
• a = b ⇔ log(a) = log(b)

Product Rule:
• log_b(xy) = log_b(x) + log_b(y)

Quotient Rule:
• log_b(x/y) = log_b(x) - log_b(y)

Power Rule:
• log_b(x^y) = y log_b(x)
• log_b(x^1/y) = log_b(x) / y

Change of Base Rule:
• log_b(x) = log_a(x) / log_a(b)

Derivatives:
• D{ln(x)} = 1 / x
• D{lg(x)} = 1 / (x ln(10))
• D{log_b(x)} = 1 / (x ln(b))

Complex:
• ln(-1) = πi
• lg(-1) = πi / ln(10)
• log_b(-1) = πi / ln(b)

A few handy corollaries:
• log_b(x) = 1 / log_x(b)
• log_b(x) / n = log_bⁿ(x)
• log_b(1/x) = log_1/b(x) = -log_b(x)
• b^log_a(x) = x^log_a(b)
• b^log_b(x) = x
• 10^lg(x) = x
• e^ln(x) = x
• log(a) × log(b) = log(b^log(a))
• log_b(a) × log_c(d) = log_c(a) × log_c(d) / log_c(b)
• log_b^p(x) = (1/p)log_b(x)
   for {b∈ℝ | b > 0, b ≠ 1} and {p∈ℝ | p ≠ 0}

Calculating the antilog:
Some calculators have an inverse– or anti–log key, many do not. After all, how far over back should calculator manufacturers bend for users who don't really understand logs?
• antilog_b(x) = b^x

Find height of object from two sightings (ASA)

Finding the height or the distance of an object from two bearings along a baseline of known length requires the solution of an ASA triangle. In the case that the angles form an isosceles triangle, the solution for height or distance is a simple matter.
Otherwise, I can't seem to find an elegant solution to this problem for a scalene triangle (doesn't mean there isn't one). What I turn up amounts to establishing the lengths of the two unknown sides per the Sine Rule, then solving for a triangle with three known sides.
If your motive is to pass an academic test, and you fear the Kelly Bundy effect, then go that way.
But if you have to do these frequently enough to want a one-step solution, then one more formula might be handy.

Acute Case:
Let
c = length of baseline (c > 0)
h = TBD height (or distance) of object
A = (0, 0)
B = (c, 0)
α = sight angle from point A (0 < α < 90°)
β = sight angle from point B (0 < β < 90°)
m = slope
then
A' = (cos(α), sin(α))
B' = (c + cos(180° - β), sin(β))
    = (c - cos(β), sin(β))
so for segment b:
m = sin(α) / cos(α) = tan(α)
and
y = tan(α) x

and for segment a
m = sin(β) / (c - cos(β) - c)
    = -tan(β)
and
y = -tan(β)(x - c)
Therefore the intersection of segments a and b is:
tan(α) x = -tan(β)(x - c)
tan(α) x = c tan(β) - tan(β) x
tan(α) x + tan(β) x = c tan(β)
x (tan(α) + tan(β)) = c tan(β)
x = c tan(β) / (tan(α) + tan(β)
so
h = c tan(α) tan(β) / (tan(α) + tan(β))

Obtuse Case:

For the obtuse case, it is frequently desirable to solve for angles α and δ. The acute case solution assumes two interior angles, so it is simply required to calculate
β = 180° - δ
so
h = c tan(α) tan(180° - δ) / (tan(α) + tan(180° - δ))

Crossing the river

A common problem for calculus students is what might be called the "crossing the river" problem. It involves crossing a river (or some other obstacle) with unequal cost (time, effort, etc.) to negotiate (travel, build, etc.) the river vs. negotiating the land. So the goal is to optimize the path.

Example:
Suppose the path to construct a refinery pipeline comes to a
perfectly straight and uniform river at some point, with the refinery
across the river, some distance upstream.
Suppose the river is 1 unit wide, and the refinery is 8 units
upstream. Also suppose the relative cost (per unit distance) for
constructing the pipeline in/over/under water is 1.6 that of
constructing it over land.

First, define in terms of distance:
Let
P = point pipeline reaches river
Q = point on opposite bank directly across river from P
R = location of refinery
S = some point on the opposite bank between Q and R
x = distance from S to R

see
crossing the river (path)

Given
PQ is 1 unit
QR is 8 unit
then
QS = 8 - x
and
Using pythagorean distance formula:
PS = √(1² + (8 - x)²)
PS = √(x² - 16x + 65)
domain 0 ≤ x ≤ 8

Second, define in terms of cost:

Given

relative cost on land = 1

relative cost in water = 1.6

Let

C(x) = total relative cost of pipe

C(x) = x + 1.6√(x² - 16x + 65)

Third, solve:

C(x) is minimized when C'(x) = 0, so

C'(x) = 0.8(2x - 16) / √(x² - 16x + 65) + 1
0 = 0.8(2x - 16) / √(x² - 16x + 65) + 1
⋮
yadda yadda
⋮
1.56x² - 24.96x + 98.84 = 0
Apply quadratic formula to find:
x ≈ 7.1994 (discard spurious root out of domain)

So
The pipeline crosses river to a point ≈ 7.2 km from refinery.

How to define a circle with three points

I was told this was a helpful way to understand how use three points to find a circle in a cartesian matrix. This method is based on the principle that the perpendicular bisectors of any two chords intersect at the center of the circle, so if you know this method you can stop reading or skip to the bottom line. I know there are more elegant ways to solve this problem, but this seems intuitive to me.

Let the points be:
A = (6, -3)
B = (16, 2)
C = (-10, 9)

Consider AB, AC and BC. By definition, each would be a chord of the circle to be found. I'll use AB and AC, but the final result would be the same for any two of them.

Let
D = Midpoint of AB:
D = (11, -1/2) *
Slope of AB = 1/2 †
Let
f(x) = line ⊥ to AB, through D:
• (y + 1/2) = -2 (x - 11) ‡
• y = -2x + 43/2
f(x) = -2x + 43/2

Let
E = Midpoint of AC:
E = (-2, 3) *
Slope of AC = -3/4 †
Let
g(x) = line ⊥ to AC, through E:
• (y - 3) = 4/3(x + 2) ‡
• y = 4x/3 + 17/3
g(x) = 4x/3 + 17/3

Let
F = center of circle to be found
F = f(x)∩g(x)
• -2x + 43/2 = 4x/3 + 17/3
• x = 19/4
• y = 4(19/4)/3 + 17/3 = 12
F = (19/4, 12)

Let
r² = square of distance from F to any of A, B or C. I'll use A:
r² = (6 - 19/4)² + (-3 - 12)² **
r² = 25/16 + 225
r² = 3625/16

SO
using standard circle form:
(x - h)² + (y - k)² = r²
where (h, k) = F,
resultant circle is:
(x - 19/4)² + (y - 12)² = 3625/16
or
(x - 4.75)² + (y - 12)² = 226.5625


The bottom line:

Let the three points be:
A = (h, k)
B = (p, q)
C = (v, w)
(k≠q and k≠w)

Then the perpendicular bisectors of AB and AC are:
ƒ(x) = (h² - 2 h x + k² - p² - q² + 2 p x) / (2k - 2q)
and
g(x) = (h² - 2 h x + k² - v² - w² + 2 v x) / (2k - 2w)

Use ƒ(x)∩g(x) to find center of circle @ ((α, β):
α = (h² (q-w) + k² (q - w) + p²w + q²w - q v² - q w² + k (v²+w²-p²-q²)) / (2(p w - q v + h (q - w) + k (v - p)))
and
β = ƒ(α) = (h² - 2 h α + k² - p² - q² + 2 p α) / (2k - 2q)
(it doesn't matter if you use ƒ(α) or g(α))

The radius of the circle (if you're interested) is:
√((h - α)² + (k - β)²)

And the circle is:
(x - α)² + (y - β)² = (h - α)² + (k - β)²
_______________
* midpoint formula: ((x₁ + x₂)/2, (y₁ + y₂)/2)
† slope formula: m = (y₁ - y₂) / (x₁ - x₂)
‡ point-slope formula: (y - y_n) = m(x - x_n)
** distance formula: c² = (x₁ - x₂)² + (y₁ - y₂)²