Find height of object from two sightings (ASA)

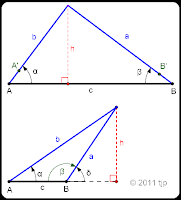
Finding the height or the distance of an object from two bearings along a baseline of known length requires the solution of an ASA triangle. In the case that the angles form an isosceles triangle, the solution for height or distance is a simple matter.
Otherwise, I can't seem to find an elegant solution to this problem for a scalene triangle (doesn't mean there isn't one). What I turn up amounts to establishing the lengths of the two unknown sides per the Sine Rule, then solving for a triangle with three known sides.
If your motive is to pass an academic test, and you fear the Kelly Bundy effect, then go that way.
But if you have to do these frequently enough to want a one-step solution, then one more formula might be handy.

Acute Case:
Let
c = length of baseline (c > 0)
h = TBD height (or distance) of object
A = (0, 0)
B = (c, 0)
α = sight angle from point A (0 < α < 90°)
β = sight angle from point B (0 < β < 90°)
m = slope
then
A' = (cos(α), sin(α))
B' = (c + cos(180° - β), sin(β))
    = (c - cos(β), sin(β))
so for segment b:
m = sin(α) / cos(α) = tan(α)
and
y = tan(α) x

and for segment a
m = sin(β) / (c - cos(β) - c)
    = -tan(β)
and
y = -tan(β)(x - c)
Therefore the intersection of segments a and b is:
tan(α) x = -tan(β)(x - c)
tan(α) x = c tan(β) - tan(β) x
tan(α) x + tan(β) x = c tan(β)
x (tan(α) + tan(β)) = c tan(β)
x = c tan(β) / (tan(α) + tan(β)
so
h = c tan(α) tan(β) / (tan(α) + tan(β))

Obtuse Case:

For the obtuse case, it is frequently desirable to solve for angles α and δ. The acute case solution assumes two interior angles, so it is simply required to calculate
β = 180° - δ
so
h = c tan(α) tan(180° - δ) / (tan(α) + tan(180° - δ))